We built a quick spreadsheet to help you easily calculate boosts if you're already familiar with the process. For a full explanation of how to calculate the value of an odds boost, read on.
Most sportsbook odds boosts are … not great. And unless you're a new user claiming the big deposit bonuses, most of them feel worthless.
Books list dozens of boosts per day that look like a deal, but really don't move the needle in terms of probability. Boosting something from +300 to +330 is only a 1.75% change in probability, and not enough to overcome the house edge.
But some boosts are mathematically advantageous. No, I'm not talking about the rare "free money" promos for existing users like Patriots-Bills over 4.5 total points or Knicks +219.5.
Instead, we're looking for smaller odds boosts offered every day that have positive expected value (EV), meaning if you bet them enough times over a large sample, you'll make money.
We usually look for boosts with 8% or more expected value (win $8 for every $100 wagered), though you can use a different threshold depending on your risk tolerance.
Fortunately, you don't need to have your own models or projections to find the expected value for many of these boosts. We can use what sportsbooks are already giving us and do some simple math to compare the true odds to the boosted odds.
Books usually have a dedicated section for boosts, and will offer the "previous odds" and the "boosted odds." But we don't care about the previous odds because sportsbooks are always trying to convince you it's a good boost. We need to figure out the real probability on our own.
Here's how to figure out if the boost is valuable or not. And here's a spreadsheet that can do most of the math for you.
After doing this for a little bit, it will often become obvious what's a good boost and what's not.
Let's pretend the boost is FanDuel taking Packersmoneyline against the 49ers from -250 to -200.
Is that a good boost?
1. Understand Implied Probability
The probabilities of anything in real life happening should add up to exactly 100%. But in sports betting, the book gets its edge by offering odds that go over 100%.
Real-life example: A coin flip at 50% heads and 50% tails adds up to 100% probability.
Sports betting example: Two point spreads at -110 each imply a probability of 52.38%. That adds up to 104.76%.
Everything over 100% is the vig — the cut the sportsbook takes to give itself an edge. We'll be removing the vig later.
2. Find Reliable Odds
OK, now we need some odds to find the true, vig-free odds of a given event. The odds you need depend on the boost.
You can use odds from any sportsbook, but to get the closest estimation of the true price, it's best to use a book that takes sharp action.
Two good examples are Nevada-based Circa Sports and Pinnacle, a Caribbean-based book licensed in England that takes sharp action (but doesn't allow U.S. bettors). Because they allow advantage bettors to bet there, their prices are generally more accurate.
If we're looking at the Packers to win boost, we can use Pinnacle's moneyline odds on that game.
If the boost is something like Josh Allen to throw for 199.5 yards and the Bills to win, you can use player props and Bills moneyline. Get creative with what markets you use.
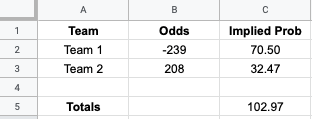
3. Convert Odds to Probability
OK, now let's convert our American odds to probabilities.
In Excel or Google Sheets, input the odds in B2 and B3 and use these formulas since the math is different for positive and negative odds:
=IF(B2>0,1/(B2/100+1),1/(1+100/ABS(B2)))
=IF(B3>0,1/(B3/100+1),1/(1+100/ABS(B3)))
The Packers are -239 at Pinnacle, and the 49ers are +208.
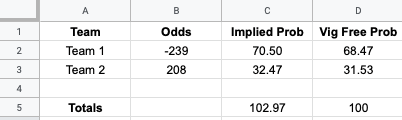
4. Remove Vig from Probability
Now to find out the true probability of an event happening, we need to remove the vig.
The process for removing the vig varies depending on the bet, but the basic idea goes like this:
- Convert the odds to probabilities, which we did.
- Divide each team's odds by the sum of the probabilities.
In Excel or Google Sheets, use these formulas in columns D2 and D3 to get the vig-free probability.
=C2/$C$5
=C3/$C$5
Two-Way Line
If it's a bet with 3-4 teams or outcomes, the process is the same — get each probability, and divide each by the total.
5. Convert Probabilities Back to Moneylines
In Excel or Google Sheets, use this formula to get the vig-free odds in columns E2 and E3.
=IF(D2/(1-D2)>=1,-1D2/(1-D2),1(1-D2)/D2)100
=IF(D3/(1-D3)>=1,-1D3/(1-D3),1(1-D3)/D3)100
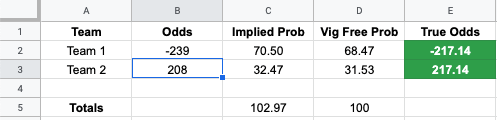
That should spit out the true odds. For a two-way market, they should be exactly the same, with one positive and one negative.
6.Calculate the Parlay, if the Boost Has Multiple Elements
Many boosts feature multiple elements, like so:
- Avalanche, Kraken, Golden Knights to all win +380
So we need to do is take the vig-free odds of each game and parlay them together. I built formulas in that sheet if you prefer to do all the math in there, or you can use our parlay calculator.
After removing the vig from each moneyline, I get a fair parlay price of +327. With the boost at +380, that gives us 12.33% expected value.

7. Plug Probability & Odds into EV Calculator
I also built an expected value calculator into the sheet, or you can use ours on site.
In Excel or Google Sheets, use this formula to get the vig-free odds in columns E2 and E3.
=((1(BOOSTEDODDS x 0.01))TRUEPROB)-((1(TRUEODDS x 0.01))TRUEPROB)

Expected value (EV) is just the amount of money you can expect to win or lose if you placed the same bet at the same probability an infinite number of times.
NHL Example
- If you're getting +380….
- And the true probability mirrors +324 odds…
- That's 12.33% expected value…
- So you can expect to win $12.33 for every $100 wagered.
8. A Brief Note on Correlation
Some bets in the same game are correlated, which makes it harder to get the true odds. Take this boost from Caesars:
- Jimmy Garoppolo over 249.5 yards & over 1.5 passing TDs (+275)
Garoppolo is more likely to throw for two TDs if he also throws for 250 yards. It's not a guarantee, but if he hits the yardage total, it means the 49ers likely had some success moving the ball and scored a few touchdowns.
The problem is that to find the true odds, you also need the other side of each bet. FanDuel has Garoppolo over 250 yards, but not under 250. So we can't get an accurate price.
Correlation can be really hard to figure out, like I touched on in this guide to same game parlays.
Another example:
- Butler To Lead At Halftime & Win Game vs. UConn (+475)
Here are FanDuel's odds for each:
- Butler 1H moneyline: +184
- Butler full game moneyline: +245
Put together the vig-free odds and you get a true line of +953. And they're offering +475, so it seems like an awful boost.
But that's not accounting for the fact that Butler is much more likely to win the game if it leads at halftime. So the price should be lower; it's just difficult to figure out how much lower.
To account for this correlation, you can use toos like the Crazy Mike SGP Devigger to find the true price on SGPs; it's a bit complicated but they have good explainers on their site.
Across the U.S., there will be at least a few boosts each day worth betting. Happy hunting!